MODUL 1
ARUS DAN TEGANGAN LISTRIK BOLAK BALIK
Sasaran Pembelajaran
Kompetensi Inti
KI 1 : Menghayati dan mengamalkan ajaran agama yang dianutnya
KI 2 : Menghayati dan mengamalkan perilaku jujur, disiplin, tanggung
jawab, peduli (gotong-royong, kerja sama, toleran, damai), santun,
responsif dan proaktif dan menunjukkan sikap sebagai bagian dari solusi
atas berbagai permasalahan dalam berinteraksi secara efektif dengan
lingkungan sosial dan alam serta dalam menempatkan diri sebagai cerminan
bangsa dalam pergaulan dunia
KI 3 : Memahami, menerapkan, dan menganalisis pengetahuan faktual,
konseptual, dan prosedural, berdasarkan rasa ingin tahunya tentang ilmu
pengetahuan, teknologi, seni, budaya, dan humaniora dengan wawasan
kemanusiaan, kebangsaan, kenegaraan, dan peradaban terkait penyebab
fenomena dan kejadian dalam bidang kerja yang spesifik untuk memecahkan
masalah.
KI 4 : Mengolah, menalar, dan menyaji dalam ranah konkret dan ranah
abstrak terkait dengan pengembangan dari yang dipelajarinya di sekolah
secara mandiri, dan mampu melaksanakan tugas spesifik di bawah
pengawasan langsung.
Kompetensi Dasar
2.1. Menunjukkan perilaku ilmiah (memiliki rasa ingin tahu; objektif;
jujur; teliti; cermat; tekun; hati-hati; bertanggung jawab; terbuka;
kritis; kreatif; inovatif dan peduli lingkungan) dalam aktivitas
sehari-hari sebagai wujud implementasi sikap dalam melakukan percobaan
dan diskusi
2.2. Menghargai kerja individu dan kelompok dalam aktivitas sehari-hari
sebagai wujud implementasi melaksanakan percobaan dan melaporkan hasil
percobaan
3.10 Menerapkan hukum kelistrikan arus bolak-balik
3.12 Menganalisis hubungan antara tegangan, impedansi, dan kuat arus pada listrik bolak-balik
4.5 Menyajikan hasil analisis yang berkaitan dengan daya dan energi listrik arus bolak-balik
Indikator
Menjelaskan konsep arus bolak balik
Menyebutkan satu contoh sumber tegangan dan arus bolak-balik
Menjelaskan persamaan fungsi waktu arus dan tegangan bolak-balik
Menghitung besarnya arus maksimum dari sebuah fungsi waktu arus bolak-balik
Menghitung besarnya arus efektif dari sebuah fungsi waktu arus bolak-balik
Menghitung besarnya arus rata-rata dari sebuah fungsi waktu arus bolak-balik
Menjelaskan cara menentukan hasil pengukuran dengan menggunakan alat ukur arus dan tegangan bolak-balik
Menentukan besarnya arus maksimum dari hasil pengukuran arus menggunakan amperemeter AC
Menentukan besarnya tegangan maksimum dari hasil pengukuran dengan menggunakan osiloskop
Menjelaskan konsep rangkaian resistif
Menjelaskan konsep rangkaian induktif
Menghitung besarnya reaktansi induktif
Menjelaskan konsep rangkaian kapasitif
Menghitung besarnya reaktansi kapasitif
Menjelaskan konsep rangkaian seri RLC
Menghitung besarnya tegangan pada rangkaian RLC
Menghitung besarnya impedansi pada rangkaian RLC
Menjelaskan konsep resonansi pada rangkaian RLC
Menyebutkan satu contoh penerapan resonansi
Menghitung besarnya frekuensi resonansi pada rangkaian RLC
Menghitung daya pada rangkaian arus bolak-balik
Menghitung tegangan keluaran dari sebuah transformator
Menghitung effisiensi transformator
Uraian Isi Pembelajaran
ARUS BOLAK BALIK
Sebelumnya kita telah mempelajari
mengenai listrik arus searah, yaitu arus dan tegangan listrik yang
besarnya dapat dianggap tetap dan mengalir dalam satu arah. Arus searah
yang juga disebut direct current (DC) contohnya dihasilkan oleh baterai.
Pada modul ini akan dibahas mengenai arus bolak-balik atau alternating
current (AC), yaitu arus dan tegangan listrik yang besarnya berubah
terhadap waktu dan dapat mengalir dalam dua arah. Arus bolak-balik
digunakan secara luas untuk penerangan maupun peralatan elektronik
seperti televisi, radio, oven microwave, dan lain-lain. Di Indonesia,
listrik arus bolak-balik disediakan oleh PLN. Pada modul ini, Anda juga
akan mempelajari beberapa komponen-komponen listrik, diantaranya
resistor, induktor, dan kapasitor, serta rangkaian yang menggunakan
komponen-komponen listrik tersebut.
GENERATOR
Generator adalah mesin yang mengubah
energi kinetik (mekanik) menjadi energi listrik. Prinsip kerja generator
adalah menghasilkan arus listrik induksi dengan cara memutar kumparan
dalam suatu medan magnetik.
Berdasarkan jenis ggl induksi atau arus listrik induksi yang dihasilkan
maka generator dapat dibedakan atas generator arus bolak-balik (AC) dan
generator arus searah (DC). Perbedaan generator arus searah dengan
generator arus bolak-balik hanyalah pada cincin luncur (cincin kolektor)
yang berhubungan dengan kedua ujung kumparan dimana generator AC
memiliki dua buah cincin yang masing-masing berhubungan dengan tiap
ujung kumparan sedangkan generator DC memiliki sebuah cincin yang
terbelah di tengahnya yang disebut cincin belah atau komutator.
Generator AC sederhana terdiri dari sebuah kumparan yang diputar dalam
suatu medan magnetik seperti gambar yang ditunjukkan gambar 1.2. Untuk
melihat bagaimana arus dibangkitkan oleh generator, perhatikan dua sisi
vertikal dari kumparan pada gambar tersebut. Agar kumparan berputar
berlawanan arah jarum jam maka sisi vertikal kiri harus mengalami gaya F
ke depan dan sisi vertikal kanan harus mengalami gaya F ke belakang.
Sesuai dengan kaidah telapak tangan untuk gaya magnetik (gaya Lorentz),
arus I pada sisi vertikal kiri haruslah ke atas, dan arus I pada sisi
vertikal kanan haruslah ke bawah, seperti ditunjukkan pada gambar
tersebut. Arah gaya F pada gambar searah dengan arah normal bidang
kumparan n. dengan demikian sudut antara arah induksi magnetik B dan
arah normal bidang n adalah θ. Dalam generator, perputaran kumparan
menyebabkan sudut θ selalu berubah, dan ini menyebabkan fluks magnetik
(Ф), yang menerobos bidang kumparan juga berubah. Pada ujung-ujung kawat
loop dibangkitkan ggl induksi (ε), yang dapat dihitung dengan
persamaan:
ε=-NBA (d cosθ)/dt
Bila loop diputar dengan kecepatan sudut ω maka θ = ωt, dan persamaan di atas dapat ditulis sebagai:
ε=-NBA (d )/dt(cos〖ωt)〗
ε=NBA ω sinωt
Jika ggl induksi maksimum antara ujung-ujung sikat sama dengan ε_m, maka persamaan di atas dapat ditulis sebagai:
ε=ε_m sin〖ωt=〗 NBA ω sinωt
Dengan ggl maksimum, ε_m, diberikan oleh:
ε_m=NBAω
Dengan ε = ggl induksi sesaat, ε_m = ggl
induksi maksimum, ω = kecepatan sudut putar dari loop dan t = lama loop
telah berputar. Nyata bahwa ggl induksi yang dihasilkan pada loop
berubah terhadap waktu setiap satu periode T=2π/ω.
ARUS DAN TEGANGAN BOLAK BALIK
Arus dan tegangan bolak-balik adalah arus
dan tegangan yang nilainya selalu berubah terhadap waktu secara
periodik. Besaran seperti ini disebut arus dan tegangan bolak-balik atau
AC (Alternating Current). Apabila pada arus searah Anda dapat
mengetahui nilai dan tegangannya yang selalu tetap. Maka, pada arus
bolak-balik Anda akan dapat mengetahui nilai maksimum yang dihasilkan
dan frekuensi osilasi yang dihasilkan oleh sumbernya. Arus dan tegangan
listrik bolak-balik berbentuk sinusoida seperti yang ditunjukkan oleh
Gambar 1.3 berikut.
Secara matematis, arus dan tegangan listrik bolak-balik tersebut dapat dinyatakan sebagai berikut:
V=V_m sinωt= V_m sin〖2πft= V_m sin〖2π t/T〗 〗
I=I_m sinωt= I_m sin〖2πft= I_m sin〖2π t/T〗 〗
Dimana:
V = tegangan sesaat (V)
I = arus sesaat (A)
Vm = tegangan maksimum (V)
Im = arus maksimum (A)
f = frekuensi (Hz)
T = periode (s)
t = waktu (s)
ωt = sudut fase (radian atau derajat)
Hubungan amplitudo tegangan atau arus
bolak-balik dengan sudut fase dapat dinyatakan secara grafik dalam
diagram fasor. Fasor adalah suatu vektor yang berputar berlawanan arah
putaran jarum jam terhadap titik asal dengan kecepatan sudut ω. Fasor
suatu besaran dilukiskan sebagai suatu vektor yang besar sudut putarnya
terhadap sumbu horizontal (sumbu x) sama dengan sudut fasenya. Nilai
maksimum besaran tersebut adalah sama dengan panjang fasor, sedangkan
nilai sesaatnya adalah proyeksi fasor pada sumbu vertikal (sumbu y).
Berikut adalah gambar diagram fasor untuk arus dan tegangan yang sudut
fasenya sama (sefase) serta gambar fungsi waktu dari arus dan tegangan
tersebut.
Sesungguhnya arus dan tegangan
bolak-balik bukanlah besaran vektor, melainkan besaran skalar.
Penggambaran arus dan tegangan bolak-balik sebagai fasor adalah untuk
mempermudah analisis rangkaian arus bolak-balik yang lebih rumit.
NILAI RATA-RATA DAN NILAI EFEKTIF
Nilai rata-rata arus bolak-balik adalah
kuat arus bolak-balik yang nilainya setara dengan kuat arus searah untuk
memindahkan sejumlah muatan listrik yang sama dalam waktu yang sama.
Arus rata-rata dinyatakan dengan:
I_r= (2I_m)/π
Sedangkan tegangan rata-rata dinyatakan dengan:
V_r= (2V_m)/π
Nilai efektif arus dan tegangan
bolak-balik ialah arus dan tegangan bolak-balik yang setara dengan arus
dan tegangan searah untuk menghasilkan jumlah kalor yang sama ketika
melalui suatu resistor dalam waktu yang sama. Secara matematis, hubungan
antara arus dan tegangan efektif dengan arus dan tegangan maksimum
dinyatakan dengan:
I_ef= I_m/√2 atau I_m= I_ef √2
V_ef= V_m/√2 atau v_m= V_ef √2
Contoh Soal
Jala-jala listrik di rumah mempunyai
tegangan 220 volt. Sebuah alat listrik dengan hambatan 50 ohm dipasang
pada jala-jala tersebut. Hitunglah:
Nilai efektif dan maksimum tegangan
Nilai efektif dan maksimum arus listrik yang mengalir
Penyelesaian:
Tegangan hasil pengukuran adalah nilai efektif, jadi Vef = 220 volt dan R = 50 Ω
Vef = 220 volt
Vmax = V_ef √2=220√2 volt
Gunakan hukum Ohm untuk menentukan kuat arus.
I_ef=V_ef/R=220/50=4,4 A
I_m=V_m/R=(220√2)/50=22/5 √2 A
Sebuah generator AC menghasilkan tegangan sebagai fungsi waktu sebagai berikut: V=200√2 sin〖50t volt.〗 Hitunglah:
Tegangan maksimum
Tegangan puncak ke puncak
Tegangan efektif
Frekuensi angular
Periode
Frekuensi
Tegangan pada saat 0,01π sekon
Penyelesaian:
Bandingkan persamaan umum tegangan dengan persamaan yang diketahui:
V=V_m sinωt volt
V=200√2 sin〖50t volt〗
V_m=200√2 volt
Tegangan puncak ke puncak sama dengan dua kali tegangan maksimum
Vpp = 2Vm = 2 . 200√2 volt = 400√2 volt
V_ef=V_m/√2=(200√2)/√2=200 volt
ω=50 rad/s
ω=2π/T → T=2π/ω=2π/50=π/25 s
f=1/T=1/(π⁄25)=25/π Hz
V pada t = 0,01 π sekon:
V=200√2 sin50t=200√2 sin〖50 (0,01π)〗
V=200√2 sin〖0,5π=200√2 sin〖〖90〗^o=〗 〗 200√2 volt
Alat Ukur Tegangan dan Arus Bolak-Balik
Tegangan dan arus listrik bolak-balik
diukur dengan voltmeter AC dan amperemeter AC (seperti terlihat pada
gambar 1.5). Dengan menggunakan alat ukur voltmeter atau amperemeter AC
besaran yang terukur adalah nilai rms (root mean squere) = akar
rata-rata kuadrat arus = ; = rata-rata dari atau nilai efektif dari
tegangan atau arus. Secara umum hasil pengukuran tegangn (V) dan arus
(I) dapat ditulis sebagai berikut:
I=(Penunjukan jarum)/(Skala maksimum)×Batas ukur maksimum
V=(Penunjukan jarum)/(Skala maksimum)×Batas ukur maksimum
Contoh Soal
Sebuah amperemeter AC digunakan untuk
mengukur kuat arus bolak-balik sehingga jarum amperemeter menunjukkan
angka seperti pada gambar di samping. Tentukanlah:
Nilai efektif
Nilai maksimum
Nilai rata-rata arus bolak-balik
Penyelesaian:
Kawat rangkaian listrik dihubungkan dengan terminal arus 0 A dan 10 A,
artinya batas ukur maksimum amperemeter 10 A. Skala amperemeter adalah 0
sampai dengan 50, sehingga jika jarum amperemeter menunjukkan angka 50
maka hasil pengukuran adalah maksimum, 10 A.
Penunjukkan amperemeter adalah nilai efektif sehingga:
I_ef=40/50×10=8 A
Nilai maksimum I_m=I_ef √2=8√2 A
Nilai rata-rata I_r=(2I_m)/π=(2×8√2)/π=16/π √2 A
Untuk melihat bentuk tegangan atau arus
sinusoidal yang dihasilkan oleh sumber bolak-balik dapat digunakan alat
ukur osiloskop (Lihat gambar 1.6). Sumbu vertikal menunjukkan nilai
tegangan atau arus yang dihasilkan oleh sumber bolak-balik dan sumbu
horizontalnya menunjukkan waktu. Dari monitor osiloskop dapat ditentukan
nilai maksimum dari tegangan atau arus listriknya dan dari sumbu
horizontal dapat ditentukan periode atau frekuensi dari sumber
bolak-baliknya. Monitor dari sebuah osiloskop terbagi-bagi menjadi
baris-baris dan kolom-kolom sehingga membentuk sebuah kotak.
Perhatikan gambar berikut!
Jika sumbu vertikal diatur pada tegangan 2 V/cm, waktu dalam arah
horizontal menunjukkan 10 ms/cm dan tiap kotak memiliki ukuran 1 cm × 1
cm. Tentukanlah:
a. tegangan maksimum sumber AC;
b. frekuensi sumber AC.
Penyelesaian:
a. Dari gambar dapat dilihat tegangan dari puncak ke puncak
Jadi, tegangan maksimumnya 4 volt.
b. Periode dari gelombang sinusoidal yang dihasilkan adalah:
Frekuensi getarnya
Jadi besar frekuens sumber AC tersebut adalah 25 Hz.
RESISTOR, INDUKTOR DAN KAPASITOR DALAM RANGKAIAN AC
GEJALA PERALIHAN PADA INDUKTOR
Tinjau rangkaian RL–seri yang dihubungkan
dengan baterei ε melalui sakelar S, seperti dalam Gambar 2 (a). Gambar 2
(b) menggambarkan beberapa contoh induktor dalam berbagai bentuk dan
ukuran yang tersedia di pasaran. Induktor berperilaku mirip massa yang
selalu menghambat gerakan, maka induktor juga selalu melawan perubahan
tegangan. Pada saat sakelar disambungkan maka dalam rangkaian terjadi
perubahan tegangan, di sinilah perlawanan induktor akan teramati.
Perilakunya berbeda dengan resistor. Hubungkan sakelar S ke a, berarti
rangkaian RL–seri tersambung dengan baterei ε, sehingga arus mengalir
dalam rangkaian dan memenuhi hukum kedua Kirchhoff:
ε= V_L+ V_R=L di/dt+iR
L di/dt= ε-iR
Sesuaikan ruas kiri hingga mendapatkan
bentuk integral dx/x. Kemudian lakukan integral dengan batas waktu saat t
= 0 adalah saat sakelar ditutup dan nilai arus i(0) = 0. Sedangkan saat
t detik dari saat sakelar ditutup nilai arus listrik pada rangkaian
adalah i(t).
ln〖((ε-iR)/ε)= -R/L t〗
Ambil nilai eksponesial dipangkatkan dengan nilai masing masing ruas persamaan tersebut yaitu:
e^(ln((ε-iR)/ε) )= ((ε-iR)/ε)=1-iR/ε=e^(-Rt/L)
i(t)= ε/R (1-e^(-Rt/L) )
Jika persamaan diatas digambarkan dalam
bentuk grafik arus terhadap waktu, diperoleh Gambar 3. Persamaan 1
menggambarkan arus pada rangkaian RL–seri sebagai fungsi waktu yaitu
merupakan proses penyimpanan energi baterei ε menjadi energi magnetik
dalam induktor, dari persamaan tersebut terlihat bahwa nilai maksimum
arus dalam rangkaian i(t) = ε/R dicapai pada t = ∞.
Nilai arus i(t) memerlukan waktu τ = L/R
bertepatan dengan nilai arus [1– (1/e)] dari nilai arus saat dimulainya
proses (t = 0). Sedangkan nilai maksimum arus pada rangkaian yaitu I =
ε/R, dapat tercapai dalam waktu t » τ, seperti pada Gambar 3. Jika
sakelar S pada gambar 2 dipindah ke titik b, berarti baterei dilepas
dari rangkaian RL–seri, persamaan hukum kedua Kirchhoff menjadi:
V_L+V_R=0
L di/dt+iR=0
di/t=-R/L dt
Integralkan persamaan tersebut dengan
batas awal t = 0 sesuai dengan i(0) = ε/R sampai dengan saat t detik
dengan arus pada induktor i(t), diperoleh :
ln[(i(t))/(ε⁄R)]=-R/L t
Ambil nilai eksponesial dipangkatkan dengan nilai masing masing ruas persamaan:
e^ln[(i(t))/(ε⁄R)] =(i(t))/[ε⁄R] =e^(-R/L t)
i(t)=ε/R e^(-Rt/L)
Persamaan 4 menggambarkan arus pada
induktor berubah terhadap waktu bila baterei dilepas dari rangkaian RL
dari kondisi arus awal pada induktor adalah arus maksimum i(0) = ε/R.
Nilai arus pada induktor akan terus menurun secara ekponensial, dari
persamaan tersebut terlihat bahwa i(t) = 0 dicapai pada t = ∞.
GEJALA TRANSIEN PADA KAPASITOR
Biasanya pengertian kapasitor adalah dua
bahan logam yang berbentuk identik yang kedua luas permukaannya dapat
berhadapan secara simetris mengikuti arah medan listrik, sehingga
memiliki kemampuan untuk menyimpan muatan listrik. Namun kenyataanya
konduktor tunggalpun memiliki kapasitansi yang merupakan ukuran daya
tampung muatan. Artinya konduktor tunggal pun mampu menampung muatan
listrik. Contoh benda berbentuk bola dapat diberi muatan karena bentuk
simetri lainnya dianggap berada di tak hingga. Kapasitor yang tersedia
di pasar dapat ditunjukkan dalam berbagai jenis dan ukuran seperti
gambar di atas. Simbol untuk kapasitor digambarkan seperti gambar
berikut.
Kapasitansi didefinisikan sebagai:
C=Q/∆V
Artinya, daya tampung muatan pada suatu
kapasitor bergantung pada beda potensial diantara kedua keping yang
berhadapan secara simetris. Nilai beda potensial ini bergantung pada
bentuk fisik dan ukuran serta jarak antara kedua keping. Hampir semua
komponen dalam rangkaian listrik memiliki kapasitansi, misal kabel,
kawat maupun resistor. Satuan SI untuk menyatakan kapasitansi adalah F
(farad), namun karena satuan ini terlalu besar untuk keperluan sehari
hari digunakan mikrofarad (ditulis μF = 10–6F), nanofarad (ditulis nF =
10–9F) dan pikofarad (ditulis pF = 10–12F).
Gambar 1.10 menunjukkan hubungan antara bentuk fisik dan arah medan listrik pada kapasitor berbentuk keping.
RANGKAIAN ARUS BOLAK-BALIK
Pada dasarnya, komponen-komponen
rangkaian listrik menunjukkan karakteristik yang berbeda ketika
dihubungkan dengan sumber tegangan searah dan ketika dihubungkan dengan
sumber tegangan bolak-balik. Karena itu, karakteristik rangkaian arus
searah berbeda dengan karakteristik rangkaian arus bolak-balik dan salah
satu perbedaan tersebut berkaitan dengan fase antara tegangan dan arus.
Pada umumnya, semua rangkaian listrik mempunyai hambatan, kapasitas, dan
induktansi meskipun pada rangkaian tersebut tidak terdapat resistor,
kapasitor, dan induktor. Akan tetapi nilai hambatan, kapasitas, dan
induktansi tersebut tergantung pada jenis komponen yang terdapat dalam
rangkaian, dan mungkin pada keadaan tertentu nilai hambatan, kapasitas,
dan induktansi tersebut dapat diabaikan, sedangkan pada keadaan lain
mungkin tidak dapat diabaikan. Secara teoritis dapat dianggap bahwa
rangkaian listrik terdiri dari rangkaian resistif, rangkaian induktif,
dan rangkaian kapasitif
RANGKAIAN RESISTIF
Rangkaian resistif merupakan rangkaian yang hanya terdiri dari sumber
tegangan (V) dengan resistor yang mempunyai hambatan R dan nilai
kapasitas (C) maupun induktansi (L) rangkaian tersebut diabaikan.
Perhatikan sebuah rangkaian arus bolak-balik yang terdiri dari sebuah
resistor dan generator AC seperti gambar berikut ini:
Tegangan pada resistor VR sama dengan tegangan generator sehingga untuk rangkaian resistif dapat ditulis:
V_R=V_m sinωt
I_R=V_m/R sinωt= I_m sinωt
Dengan demikian akan berlaku juga hubungan sebagai berikut:
I_m=V_m/R
I_ef=V_ef/R
Karena rangkaian resistif dianggap tidak mempunyai induktansi dan
kapasitas, maka rangkaian resistif tidak dipengaruhi oleh perubahan
medan magnet di sekitarnya. Berdasarkan hal tersebut, maka pada
rangkaian resistif, arus dan tegangan bolak-balik mempunyai fase yang
sama atau beda fasenya nol.
RANGKAIAN INDUKTIF
Rangkaian induktif merupakan rangkaian yang hanya terdiri dari sumber
tegangan (V) dengan induktor yang mempunyai induktansi L dan nilai-nilai
hambatan (R) maupun kapasitas (C) rangkaian tersebut diabaikan, seperti
ditunjukkan gambar berikut:
Arus yang mengalir pada rangkaian
induktif murni berubah terhadap waktu yang memenuhi persamaan I=I_m
sin〖ωt,〗 sehingga pada induktor terinduksi gaya gerak listrik yang
memenuhi persamaan:
ε_ind=-L dI/dt=-L d(I_m sinωt )/dt
Karena pada rangkaian induktif, hambatan
rangkaian (R) dan kapasitasnya (C) diabaikan, maka tidak ada penurunan
potensial (IR) pada induktor, sehingga tegangan sumber V sama dengan
gaya gerak listrik induksi 〖-ε〗_ind= V_L, yaitu:
V=-ε_ind atau V = VL
V_m sinωt= L dI/dt → dI=V_m/L sin〖ωt dt〗
∫▒〖dI= ∫▒〖V_m/L sin〖ωt dt〗 〗〗
I=-V_m/ωL cos〖ωt, dimana cos ωt= -〖sin(〗〖ωt-π/2)〗 〗
I=V_m/ωL sin (ωt-π/2)= I_m 〖 sin〗(ωt-π/2)
Jadi pada rangkaian induktif arus listrik
mempunyai fase yang berbeda dengan tegangan. Sesuai dengan persamaan I
dan V di atas, maka beda fase antara arus dan tegangan pada rangkaian
induktif adalah ∅=π/2. Dalam hal ini, pada rangkaian induktif, tegangan
(V) mendahului arus (I) dengan beda fase sebesar π/2 atau 90o.
Meskipun pada rangkaian induktif tidak terdapat resistor, tetapi pada
rangkaian ini terdapat sebuah besaran yang mempunyai sifat yang sama
dengan hambatan listrik, yaitu reaktansi induktif, yang besarnya dapat
ditentukan sebagai berikut:
X_L=ωL=2πfL
Dengan:
X_L = reaktansi induktif (Ω)
ω = kecepatan sudut (rad/s)
f = frekuensi sumber AC (Hz)
L = induktansi induktor (H)
RANGKAIAN KAPASITIF
Rangkaian kapasitif adalah rangkaian yang hanya terdiri dari sumber
tegangan (V) dengan kapasitor yang mempunyai kapasitas C dan nilai-nilai
hambatan (R) dan induktansi (L) rangkaian tersebut diabaikan, seperti
ditunjukkan gambar berikut ini:
Pada rangkaian kapasitif murni, tegangan
yang dipasang pada kapasitor berubah terhadap waktu sesuai dengan
persamaan V=V_m sin〖ωt,〗 sehingga muatan yang tersimpan pada kapasitor
memenuhi persamaan berikut:
Q=CV=C(V_m sinωt )=CV_m sinωt
Sehingga arus listrik pada kapasitor ditentukan sebagai berikut:
I=dQ/dt=d(CV_m sinωt )/dt
I=ωC V_m cosωt
I=ωC V_m sin〖(ωt+π/2)= I_m 〗 sin(ωt+π/2)
Sesuai dengan persamaan I dan V di atas,
maka pada rangkaian kapasitif, arus mempunyai beda fase sebesar ∅=π/2
dengan tegangan. Dalam hal ini, arus mendahului tegangan dengan beda
fase sebesar π/2 atau 90o.
Seperti juga pada rangkaian induktif, maka pada rangkaian kapasitif
terdapat sebuah besaran reaktansi yang disebut reaktansi kapasitif dan
besarnya dapat ditentukan sebagai berikut:
X_C=1/ωC=1/2πfC
Dengan:
X_C = reaktansi kapasitif (Ω)
C = kapasitas kapasitor (F)
Contoh Soal
Sebuah rangkaian arus bolak-balik yang
bersifat induktif murni terdiri dari induktor dengan induktansi L = 25
mH dan sumber tegangan AC dengan tegangan efektif 150 V. berapakah:
Reaktansi induktifnya
Kuat arus efektif rangkaian jika frekuensi sumber 50 Hz.
Penyelesaian:
X_L=ωL=2πfL=2π(50)(25×〖10〗^(-3) )=7,85 Ω
I_ef=V_ef/X_L =150/7,85=19,1 A
Sebuah kapasitor 8 μF dihubungkan dengan
sebuah sumber tegangan AC yang tegangan efektifnya 150 V dan
frekuensinya f = 50 Hz. Berapakah:
Reaktansi kapasitif
Arus efektif di dalam rangkaian
Penyelesaian:
X_C=1/ωC=1/2πfC=1/(2π(50)(8×〖10〗^(-6)))=397,89 Ω
I_ef=V_ef/X_C =150/397,89=0,38 A
RANGKAIAN SERI R-L-C
Pada kegiatan belajar sebelumnya telah
dibahas bagaimana pengaruh resistor, induktor, dan kapasitor yang
dihubungkan secara terpisah dengan sebuah sumber arus bolak-balik I=I_m
sinωt. Sekarang akan ditinjau, apa yang akan terjadi jika ketiga elemen
tersebut dihubungkan secara seri, yang sering disebut rangkaian seri
RLC seperti gambar di atas.
HUBUNGAN VR, VL, VC, DAN V PADA RANGKAIAN SERI RLC
Untuk menentukan hubungan VR, VL, dan VC
digunakan diagram fasor. Perhatikan bahwa karena ketiga elemen
berhubungan seri, maka arus yang mengalir melalui semua elemen sama
besar, yaitu I=I_m sinωt. Dengan kata lain arus bolak-balik di semua
titik pada rangkaian seri RLC memiliki nilai maksimum dan fase yang
sama. Akan tetapi tegangan pada masing-masing elemen akan memiliki nilai
dan fase yang berbeda. Tegangan pada resistor VR sefase dengan arus I,
tegangan pada induktor VL mendahului arus π/2 rad atau 90o, dan tegangan
pada kapasitor tertinggal dari arus π/2 rad atau 90o. Dengan demikian
dapat ditulis:
V_R=I_m R sinωt= V_mR sinωt
V_L=I_m X_L 〖sin 〗〖(ωt〗+〖90〗^o)= V_mL sin〖 (ωt〗+〖90〗^o)
V_C=I_m X_C sin〖 (ωt〗-〖90〗^o)= V_mC sin〖 (ωt〗-〖90〗^o)
Jika ditetapkan sudut ωt pada sumbu x,
maka diagram fasor untuk arus I, tegangan VR, VL, dan VC akan tampak
seperti gambar berikut.
Sesuai dengan hukum Kirchoff, tegangan
antara ujung-ujung rangkaian seri RLC, yaitu VAB = V adalah jumlah fasor
antara VR, VL, dan VC. penjumlahan fasor tersebut menghasilkan besar
tegangan total, yaitu:
V=√(V_R^2+(V_L-V_C )^2 )
Tampak jelas pada gambar bahwa beda sudut fase antara arus dan tegangan θ memenuhi hubungan:
tan〖θ=(V_L-V_C)/V_R 〗
IMPEDANSI RANGKAIAN SERI R-L-C
Pada rangkaian DC umumnya hanya akan
ditemukan satu macam hambatan yaitu resistor murni R, nilai hambatan
total dari beberapa resistor yang terhubung secara seri adalah
penjumlahan secara aljabar (skalar) masing-masing hambatan tersebut.
Pada rangkaian AC, terdapat resistor, induktor, dan kapasitor dalam
rangkaian. Efek hambatan total yang dihasilkan oleh R, XL, dan XC dalam
rangkaian AC disebut impedansi (Z). Nilai Z tidak dapat dihitung dengan
penjumlahan aljabar (skalar) seperti pada arus searah. Untuk menentukan
nilai Z digunakan persamaan berikut:
V=√(V_R^2+(V_L-V_C )^2 )
IZ=√((IR)_^2+(〖IX〗_L-〖IX〗_C )^2 )
IZ=I√((R)_^2+(X_L-X_C )^2 )
Z=√((R)_^2+(X_L-X_C )^2 )
Beda sudut fase antara kuat arus I dengan tegangan V adalah:
tan〖θ=(V_L-V_C)/V_R 〗=(〖IX〗_L-〖IX〗_C)/IR
tan〖θ=(X_L-X_C)/R〗
Dengan menggunakan kedua persamaan di atas dapat dibuat diagram fasor untuk impedansi seperti tampak pada gambar berikut.
Contoh Soal
Rangkaian R-L-C seri dengan R = 80 ohm,
XL = 100 ohm, dan Xc =40 ohm. Rangkaian ini dihubungkan dengan tegangan
bolak-balik dengan tegangan efektif 220 V. Tentukanlah:
a. impedansi rangkaian;
b. arus efektif yang mengalir pada rangkaian;
c. tegangan efektif antara ujung-ujung induktor.
Penyelesaian:
Impedansi rangkaian
Arus efektif pada seluruh rangkaian
Tegangan efektif antara ujung-ujung induktor
RESONANSI PADA RANGKAIAN R-L-C
Resonansi pada rangkaian seri R-L-C
terjadi ketika XL = XC. Keadaan ini menyebabkan impedansi rangkaian Z
memiliki harga minimum yang bernilai sama dengan hambatan murni R.
Adapun arus dalam rangkaian menjadi maksimum. Garis singgung antara
kurva Z dan garis linear R merupakan titik terjadinya frekuensi
resonansi. Di titik tersebut besaran Z bernilai minimum. Perhatikan
gambar berikut.
Saat terjadinya resonansi,
Oleh karena , maka diperoleh frekuensi resonansi
Rangkaian resonansi dapat dijumpai pada
rangkaian penala, caranya dengan mengubah-ubah frekeunsi melalui
kondensator variabel. Jika frekuensinya sesuai, frekuensi gelombang
radio akan di tangkap.
Contoh Soal
Pada frekuensi berapakah sebuah rangkaian R-L-C seri yang dihubungkan
bertegangan bolak-balik akan beresonansi. Apabila R = 80 ohm, L = 1
henry, dan C = 1 F?
Penyelesaian:
Diketahui
R = 80 ohm
L = 1 henry
C = 1 F = 10-6 F
Ditanyakan: f = …?
Jawab:
Frekuensi resonansi terjadi jika:
Oleh karena , maka diperoleh frekuensi resonansi
Jadi besar frekuensi resonansinya adalah Hz.
DAYA PADA ARUS LISTRIK BOLAK-BALIK
Induktor dan kapasitor yang terpasang
pada rangkaian arus bolak-balik membutuhkan tambahan energi listrik.
Daya yang diserap dalam rangkaian resistif (Z) besarnya adalah
Dan dalam rangkaian R-L-C seri adalah
c
Persamaan di atas disebut juga sebagai daya semu. Adapun daya yang sesungguhnya atau daya rata-rata adalah
Keterangan
= beda fase antara arus dan tegangan
Cos = faktor daya
Contoh Soal
Sebuah rangkaian seri R–L-C dengan R = 30 Ω, L = 0,6 H dan C = 500 F
dihubungkan dengan sumber tegangan bolak-balik yang memiliki V = 300 sin
100t Volt. Tentukan:
Impedansi rangkaian
Daya rata-rata yang diserap rangkaian
Penyelesaian:
Diketahui:
R = 30 Ω
L = 0,6 H
C = 500 F = 500 x 10-6 F = 5 x 10-4 F
V = 300 sin 100t Volt
Ditanyakan:
Z = …?
P = …?
Jawab:
Dari tegangan V = 300 sin 100 t Volt, didapatkan:
Vm = 300
= 100
Beda sudut fase
Impedansi rangkaian
XL = .L = 100 . 0,6 = 60 Ω
Sehingga:
Daya rata-rata yang diserap rangkaian adalah
Sehingga:
Jadi besar daya rata-rata yang diserap adalah 540 W.
TRANSFORMATOR
Apakah transformator itu? Dalam kehidupan
sehari-hari tentunya kamu sering mendengar atau mungkin telah
menggunakan transformator. Transformator adalah alat yang digunakan
untuk mengubah tegangan bolak-balik (AC) dari satu nilai tertentu
menjadi nilai yang diinginkan.
Transformator atau trafo terdiri dari
pasangan kumparan primer dan sekunder yang terpisah dan dililitkan pada
inti besi lunak. Kumparan primer berfungsi sebagai input dan kumparan
sekunder berfungsi sebagai output. Prinsip dasar cara kerja
transformator adalah hukum induksi Faraday. Kumparan primer dihubungkan
ke suatu sumber arus bolak-balik yang besar arus listriknya senantiasa
berubah terhadap waktu. Arus pada kumparan primer ini bekerja
seolah-oleh mengalirkan atau memutuskan arus searah secara
berulang-ulang sehingga terjadi perubahan garis-garis gaya magnet yang
memotong kumparan sekunder. Akibatnya, timbul GGL induksi dalam kumparan
sekunder yang berfungsi sebagai output dengan mengalirkan arus listrik
induksi. Dengan menentukan jumlah lilitan yang
sesuai untuk tiap kumparan, dapat dihasilkan GGL kumparan sekunder yang berbeda dengan GGL pada kumparan primer.
Hubungan antara tegangan dengan jumlah lilitan kumparan pada sebuah
transformator dapat ditulis secara matematis sebagai berikut.
dengan:
Vs = tegangan sekunder (volt)
Vp = tegangan primer (volt)
Ns = lilitan sekunder (lilitan)
Np = lilitan primer (lilitan)
Contoh Soal
Sebuah tarfo step-up kumparan primernya terdiri atas 50 lilitan dan
kumparan sekundernya 100 lilitan. Jika tegangan primernya 110 V,
berapakah tegangan pada kumparan sekundernya?
Penyelesaian
Diketahui:
Np = 50 lilitan
Ns= 100 lilitan
Vp = 110 V
Ditanyakan: Vs = ?
Jawab:
Jadi, tegangan pada kumparan sekunder adalah 220 V.
Persamaan Trafo untuk Transformator Ideal
Apakah jumlah energi yang masuk sama
dengan jumlah energi yang keluar? Menurut hukum kekekalan energi,
apabila transformator itu adalah transformator ideal maka jumlah energi
yang masuk ke dalam sebuah transformator sama dengan jumlah energi yang
keluar dari transformator itu. Akibatnya, daya listrik yang ada pada
kumparan primer (Pp) adalah sama dengan daya listrik yang ada pada
kumparan sekunder (Ps). Dengan demikian, secara matematis dapat ditulis:
Pp = Ps
Karena Pp = Vp Ip dan Ps = Vs Is, maka:
Vp Ip = Vs Is
Keterangan:
Pp = daya pada kumaparan primer (watt)
Ps = daya pada kumparan sekunder (watt)
Contoh Soal
Sebuah trafo step-down dihubungakan dengan sumber tegangan 220 V. Trafo
ini digunakan untuk menyalakan lampu bertegangan 10 V. Jika kuat arus
listrik yang melalui lampu 4 A, berapakah kuat arus listrik yang melalui
kumparan primer?
Penyelesaian:
Diketahui:
Vp = 220 V
Vs = 10 V
Is = 4 A
Ditanyakan: Ip =….. ?
Jawab:
Vp Ip = Vs Is
Jadi, arus listrik yang melewati kumparan primer adalah 0,182 A.
Efisiensi Transformator
Inti transformator terbuat dari
pelat-pelat besi. Ketika suatu tegangan bolak-balik dihubungkan pada
transformator maka akan dihasilkan garis-garis gaya magnet yang selalu
berubah. Hal ini dapat menyebabkan timbulnya arus pusat pada inti
tarnsformator. Inti transformator terbuat dari besi yang bersifat
sebagai penghantar yang memiliki hambatan listrik sehingga timbul
kehilangan energi dalam bentuk kalor. Selain itu, kumparan primer dan
sekunder yang terbuat dari kawat tembaga dan bersifat sebagai penghantar
dengan nilai hambatan listrik tertentu juga menimbulkan kehilangan
energi dalam bentuk kalor. Dalam transformator selalu timbul kalor
sehingga energi listrik yang keluar dari transformator selalu lebih
kecil daripada energi listrik yang masuk ke transformator. Sebagian
energi listrik itu berubah menjadi kalor. Keadaan ini merupakan sesuatu
yang tidak dapat dihindarkan.
Efisiensi transformator didefinisikan sebagai perbandingan antara daya
listrik yang keluar dari transformator dengan daya listrik yang masuk ke
transformator.
Transformator adalah alat atau mesin yang sangat efisien. Efisiensi transformator dapat mencapai 99%.
Contoh Soal
Sebuah tarnsformator memiliki tegangan primer 220 V dan tegangan
sekunder 110 V. Apabila kuat arus yang mengalir melalui tegangan primer
sebesar 0,2 A, ternyata kuat arus yang mengalir pada kumparan sekunder
menjadi 0,3 A. Berapakah efisiensi transformator itu?
Jawaban:
Diketahui:
Vp = 220 V
Vs = 110 V
Ip = 0,2 A
Is = 0,3 A
Ditanyakan: = ….. ?
Jawab:
Jadi, efisiensi transformator adalah 75%.
Rangkuman
Latihan Soal-soal
1. Jala-jala listrik di rumah mempunyai
tegangan 220 volt. Sebuah alat listrik dengan hambatan 50 ohm dipasang
pada jala-jala tersebut. Hitunglah:
Nilai efektif dan maksimum tegangan
Nilai efektif dan maksimum arus listrik yang mengalir
2. Sebuah generator AC menghasilkan tegangan sebagai fungsi waktu sebagai berikut: V=100√2 sin〖10t volt.〗 Hitunglah:
Tegangan maksimum
Tegangan puncak ke puncak
Tegangan efektif
Frekuensi angular
Periode
Frekuensi
Tegangan pada saat 0,01π sekon
3.
Sebuah amperemeter AC digunakan untuk
mengukur kuat arus bolak-balik sehingga jarum amperemeter menunjukkan
angka seperti pada gambar di samping. Tentukanlah:
Nilai efektif
Nilai maksimum
Nilai rata-rata arus bolak-balik
4. Perhatikan gambar berikut!
Jika sumbu vertikal diatur pada tegangan 4 V/cm, waktu dalam arah
horizontal menunjukkan 12 ms/cm dan tiap kotak memiliki ukuran 1 cm × 1
cm. Tentukanlah:
a. tegangan maksimum sumber AC;
b. frekuensi sumber AC.
5. Sebuah rangkaian arus bolak-balik yang
bersifat induktif murni terdiri dari induktor dengan induktansi L = 10
mH dan sumber tegangan AC dengan tegangan efektif 100 V. berapakah:
Reaktansi induktifnya
Kuat arus efektif rangkaian jika frekuensi sumber 10 Hz.
6. Sebuah kapasitor 2 μF dihubungkan
dengan sebuah sumber tegangan AC yang tegangan efektifnya 100 V dan
frekuensinya f = 10 Hz. Berapakah:
Reaktansi kapasitif
Arus efektif di dalam rangkaian
7. Rangkaian R-L-C seri dengan R = 30
ohm, XL = 80 ohm, dan Xc = 40 ohm. Rangkaian ini dihubungkan dengan
tegangan bolak-balik dengan tegangan efektif 220 V. Tentukanlah:
a. impedansi rangkaian;
b. arus efektif yang mengalir pada rangkaian;
c. tegangan efektif antara ujung-ujung induktor.
8. Pada frekuensi berapakah sebuah
rangkaian R-L-C seri yang dihubungkan bertegangan bolak-balik akan
beresonansi. Apabila R = 60 ohm, L = 1 henry, dan C = 100 F?
9.
Sebuah rangkaian seri R–L-C dengan R = 10 Ω, L = 0,6 H dan C = 400 F
dihubungkan dengan sumber tegangan bolak-balik yang memiliki V = 100 sin
100t Volt. Tentukan:
Impedansi rangkaian
Daya rata-rata yang diserap rangkaian
10. Sebuah tarnsformator memiliki
tegangan primer 220 V dan tegangan sekunder 110 V. Apabila kuat arus
yang mengalir melalui tegangan primer sebesar 0,4 A, ternyata kuat arus
yang mengalir pada kumparan sekunder menjadi 0,6 A. Berapakah efisiensi
transformator itu?
Umpan Balik
Kriteria Penilaian Tes
Skor Kriteria
5 Memberikan suatu penyelesaian lengkap dan benar
4 Memberikan suatu penyelesaian yang benar, sedikit cacat, tetapi memuaskan
3 Memberikan suatu penyelesaian yang benar, banyak cacat, tetapi hampir memuaskan
2 Memberikan suatu penyelesaian yang ada unsur benarnya, tetapi tidak memadai
1 Mencoba memberikan suatu penyelesaian, tetapi salah total
0 Tidak mencoba memberikan penyelesaian sama sekali
Rumus untuk menghitung skor akhir tes
Contoh:
Dalam tes yang terdiri dari 5 buah soal, dengan menggunakan kriteria penilaian tes, anda mendapatkan nilai sebagai berikut.
No Tes Nilai
1 4
2 5
3 5
4 5
5 5
Jumlah 24
Karena jumlah soal adalah 5, maka nilai skor maksimumnya adalah 5 × 5 = 25.
Jadi nilai Anda adalah 96.
Konversi Dari Skor 1-100 Ke 1-4
INTERVAL HASIL KONVERSI PREDIKAT
96 – 100 4.00 A
91 – 95 3.66 A-
86 – 90 3.33 B+
81 – 85 3.00 B
75 – 80 2.66 B-
70 – 74 2.33 C+
65 – 69 2.00 C+
60 – 64 1.66 C-
55 – 59 1.33 D+
≤ 54 1.00 D
Jadi dari konversi di atas, nilai yang Anda peroleh adalah 4,00 dengan predikat A.
sumber : https://fisikakontekstual.wordpress.com/materi-arus-dan-tegangan-listrik-bolak-balik/







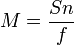
 = Pembesaran
= Pembesaran = Titik dekat (cm)
= Titik dekat (cm)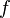 = Fokus lup (cm)
= Fokus lup (cm)



 = Pembesaran mikroskop
= Pembesaran mikroskop = Pembesaran oleh lensa objektif
= Pembesaran oleh lensa objektif = Pembesaran oleh lensa okuler (seperti perbesaran pada lup)
= Pembesaran oleh lensa okuler (seperti perbesaran pada lup) = Jarak fokus lensa okuler
= Jarak fokus lensa okuler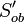 = jarak bayangan oleh lensa objektif
= jarak bayangan oleh lensa objektif = jarak benda di depan lensa objektif
= jarak benda di depan lensa objektif = jarak lensa objektif dan lensa okuler
= jarak lensa objektif dan lensa okuler

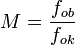

 = Jarak fokus lensa objektif
= Jarak fokus lensa objektif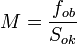


 = Jarak fokus lensa pembalik
= Jarak fokus lensa pembalik























